Arıkan教授在文献[1]提出了串行抵消SC译码算法。SC译码算法类似一个深度优先搜索的算法，其根据两个判决函数进行迭代计算最大似然对数比LLR，两个判决函数分别叫做f函数和g函数。下面是这两个公式的计算方法：

$$
\begin{align}
f\left( a,b \right)=\ln \left( \frac{1+{ {e}^{a+b}}}{ { {e}^{a}}+{ {e}^{b}}} \right)
\end{align}
$$

$$
\begin{align}
g\left( a,b,{ {u}{s}} \right)={ {\left( -1 \right)}^{ { {u} {s}}}}a+b
\end{align}
$$

其中，$a,b\in R,{ {u}_{s}}\in \left{ 0,1 \right}$。LLR的递归运算借助函数f和g表示如下：

$$
\begin{align}
L_{N}^{\left( 2i-1 \right)}\left( y_{1}^{N},\hat{u}{1}^{2i-2} \right)=f\left( L {N/2}^{\left( i \right)}\left( y_{1}^{ {N}/{2};},\hat{u}{1,o}^{2i-2}\oplus \hat{u} {1,e}^{2i-2} \right),L_{N/2}^{\left( i \right)}\left( y_{ {N}/{2};+1}^{N},\hat{u}_{1,e}^{2i-2} \right) \right)
\end{align}
$$

$$
\begin{align}
L_{N}^{\left( 2i \right)}\left( y_{1}^{N},\hat{u}{1}^{2i-1} \right)=g\left( L {N/2}^{\left( i \right)}\left( y_{1}^{ {N}/{2};},\hat{u}{1,o}^{2i-2}\oplus \hat{u} {1,e}^{2i-2} \right),L_{N/2}^{\left( i \right)}\left( y_{ {N}/{2};+1}^{N},\hat{u}{1,e}^{2i-2} \right),{ { {\hat{u}}} {2i-1}} \right)
\end{align}
$$

递归的终止条件为当$N=1$时，即到达了信道$W$端，此时$L_{1}^{\left( 1 \right)}\left( { {y}{j}} \right)=\ln \frac{W\left( { {y}{j}}|0 \right)}{W\left( { {y}_{j}}|1 \right)}$。

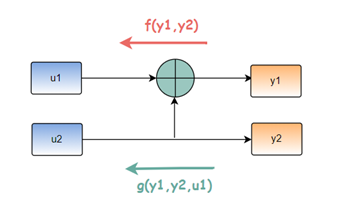
SC译码算法依靠一个蝶形单元，如图10，在计算的时候不断进行递归，但是必须是先计算出蝶形单元的上行比特，才能够调用g函数求出下行比特。即图10中必须使用f函数计算出u1，之后才能够通过g函数求出u2。在实际的计算过程中，从接收的比特进行递归执行f函数和g函数，其中假如编码每次进行一次极化，在译码阶段都会多一次递归的计算，中间的计算值就是进行极化的临时值，在一整个蝶形结构中体现，是一个深度优先的算法。

SCL译码算法[3]类似树的广度优先遍历，它的好处就是能够进行剪枝操作，不用计算所有的节点。它从根节点开始往树底部进行广度遍历搜索，每一层会计算出一个估计比特，然后在这个估计比特的基础上往下进行估计下一个比特的值，另外，SCL译码算法还增加了惩罚因子，对于惩罚因子过高的节点，我们可以直接跳过它以及它子节点的计算，因为它是正确的码的可能性极低，这样排除了不可能的路径，同时，这也能达到对树进行剪枝的效果，提高译码的速度。图11展示了进行SCL译码的基本过程：