在通信过程中，物理层传输的就是电信号，假如我们只用0和1传输信号，并且这些信道互相都没有关系，我们称为二进制离散无记忆信道。信道模型是研究信道编码的基础，常见的几种信道模型分别有：二进制删除信道（BEC）、二进制对称信道（BSC）、高斯信道（AWGN）。设信道的输入和输出分别是长为N的序列，输入是x，输出是y，其信道的转移概率满足：
$$
p\left( {y|x} \right) = \sum_{i=1}^N p\left( {y_{i} | x_{i}} \right)
$$

无损信道

无论发送任何消息，接受方都能够准确无误的接收到，并且不会发生错误，那么这个信道就可以说是一个无损信道。最简单的的就是下面这个模型，不管发送者发送的是0还是1，接收者接受的都是一致的。

假如我们随机进行传输0或者1的数据，其传输的数值图为下面：

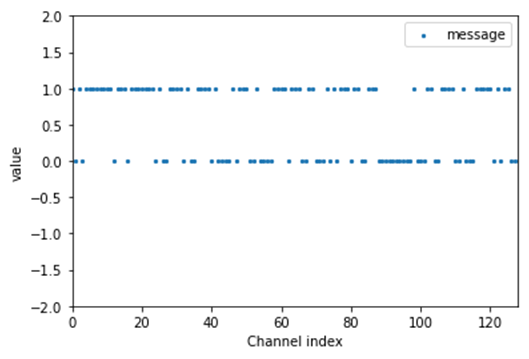
二进制删除信道

二进制删除信道，简记为BEC（Binary Erasure Channel ）。ϵ称为删除概率，表示有ϵ的概率这个信号会丢失。当接收方得到一个位，它是100%确定的位是正确的。只有当位被擦除时，才会出现唯一的混淆。对于二进制离散无记忆信道，我们有ϵ的概率丢失0或者1的比特位。

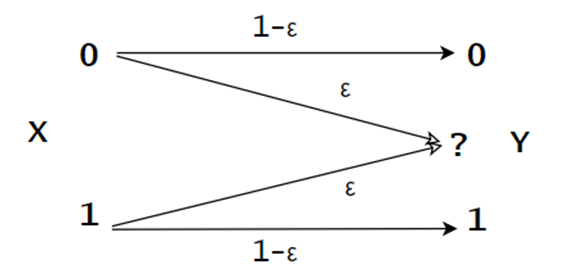
BEC的信道容量为：

$$
C= 1 - \epsilon
$$

二进制对称信道

二进制对称信道，简记为BSC（Binary Symmetric Channel ）。p称为交叉概率，表示有p的概率会导致传输过程中0信号和1信号的错乱。（错乱的意思是发送0，收到却是1；或者发送1，收到却是0）

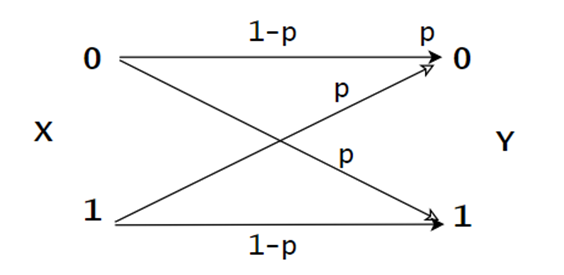
BSC的信道容量为：

$$
C = \log n + q\log q + (1-q) \log \frac {1-q}{n-1}
$$

加性高斯白噪声信道

高斯信道，常指加权高斯白噪声（AWGN）信道。这种噪声假设为在整个信道带宽下功率谱密度（PDF）为常数，并且振幅符合高斯概率分布。

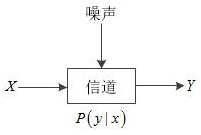
一般来说，高斯信道需要配合BPSK机制进行调制，在传输之前，我们对0和1比特进行变换，比特0会变成1，比特1变成-1，而这个将比特进行转换的过程就是BPSK调制，最后在BPSK调制后再加上高斯噪声，实际的模型如下：。

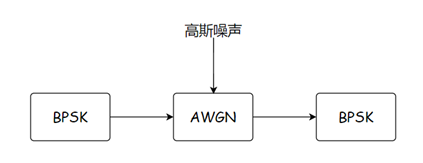
通过BPSK调制之后0比特和1比特都会向1和-1这两个临界线靠经，在这个情况下传入高斯信道，即使存在高斯噪声进行影响，我们也能够减小它的影响，在解码端对码字进行BPSK解调，能够得到较高的准确率。

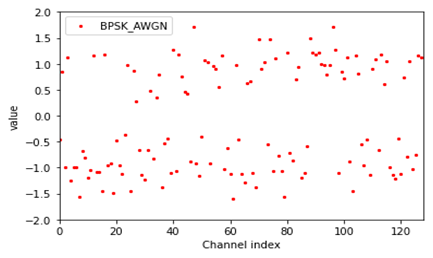
由图可以发现，值靠近1的信号表示原来的信号是0，值靠近-1的信号表示原来的信号是1。这样的好处是在传输过程中减少高斯噪声的干扰，让传输的信号更加稳定。

特别的，5G标准要求信道编码至少能够在加性高斯白噪声信道（AWGN）下进行传输。