RSA算法
RSA加密算法是一种非对称加密算法,在公开密钥加密和电子商业中被广泛使用。
对极大整数做因数分解的难度决定了 RSA 算法的可靠性。换言之,对一极大整数做因数分解愈困难,RSA 算法愈可靠。假如有人找到一种快速因数分解的算法的话,那么用 RSA 加密的信息的可靠性就会极度下降。但找到这样的算法的可能性是非常小的。今天只有短的 RSA 钥匙才可能被强力方式破解。到当前为止,世界上还没有任何可靠的攻击RSA算法的方式。只要其钥匙的长度足够长,用RSA加密的信息实际上是不能被破解的。
公钥/双密钥/非对称 加密 涉及到两个密钥的使用:
- 一个公钥, 可以被任何人知道,用于加密消息和验证签名
- 一个私钥, 只有接收方才知道,用于解密消息和创造签名

RSA实现过程
1. 公钥与私钥的产生
生成公钥e和私钥d的步骤如下:
- 随意选择两个大的质数$p$和$q$,$p$不等于$q$,计算$n=pq$。
- 根据欧拉函数,求$r = \varphi (N) = \varphi (p)\varphi (q) = (p - 1)(q - 1)$
- 选择一个小于$r$的整数$e$,使$e$与$r$互质。并求得$e$关于$r$的模反元素,命名为$d$(求$d$令$ed \equiv 1(\bmod ;r)$)。(模反元素存在,当且仅当$e$与$r$互质)
- 将$p$和$q$的记录销毁
经过上面四个步骤最终可以得到公钥$(n,e)$和私钥$(n,d)$。
接收消息的人将自己的公钥$(n,e)$发送给发送消息的人,发送的人使用这个公钥加密信息发送给接收方,而接收方将私钥$(n,d)$保存起来用于解密。
下面实现RSA类
参考资料:
实验步骤与结果
1.实现大整数类
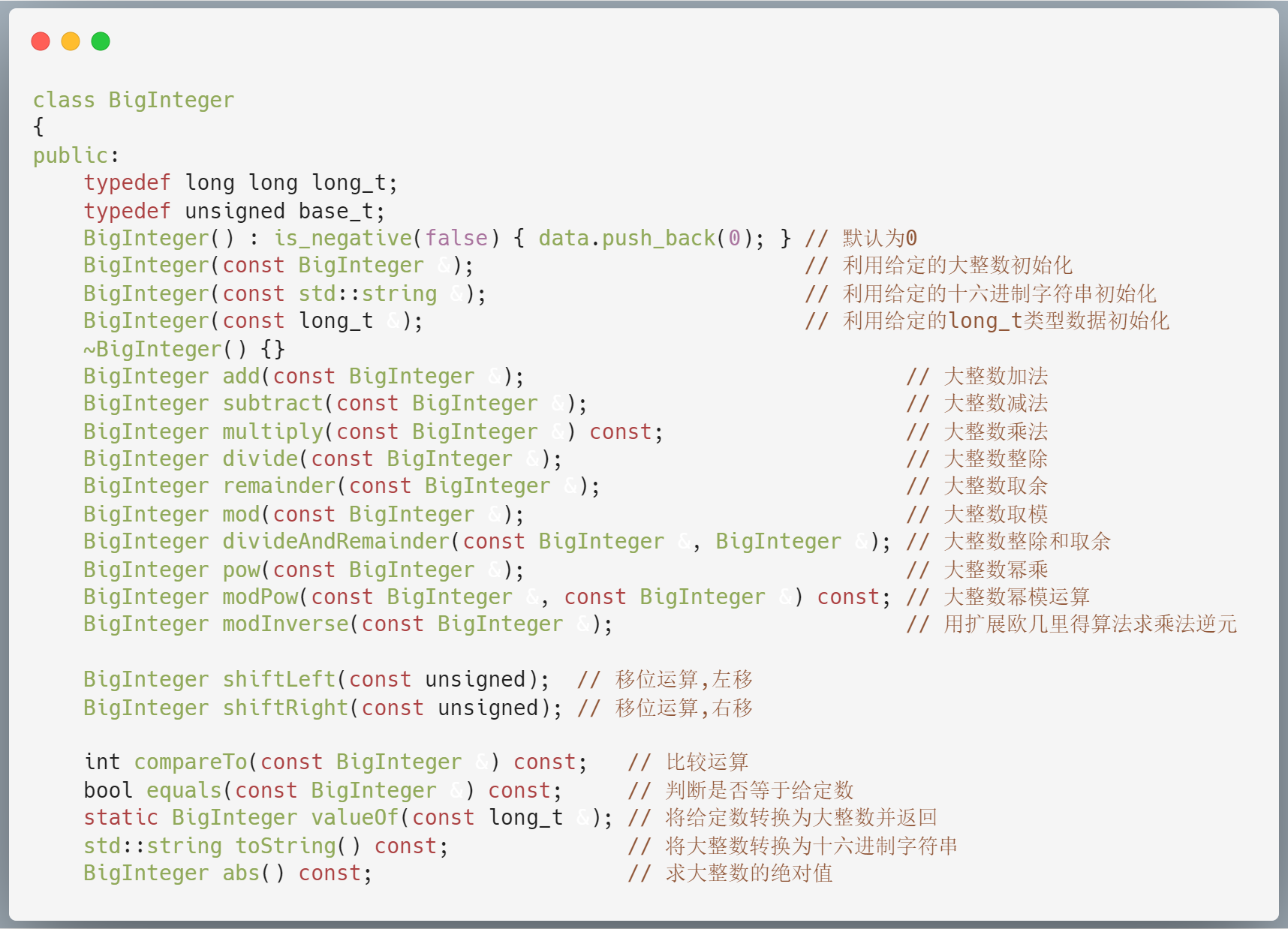
因为该加密算法涉及的数可能很大,而C++中并没有像Java一样,内置大整数类BigInteger,故需自己实现,这里我参考了网上的一些资料设计了BigInteger类,实现了加减乘除以及模幂等运算,也实现了运算符重载,具体参考实现的方法如下:
2. 设计RSA类
编写rsa.h头文件,定义RSA类,其中包含的成员以及成员函数如下:
下面分别实现上述的各个方法
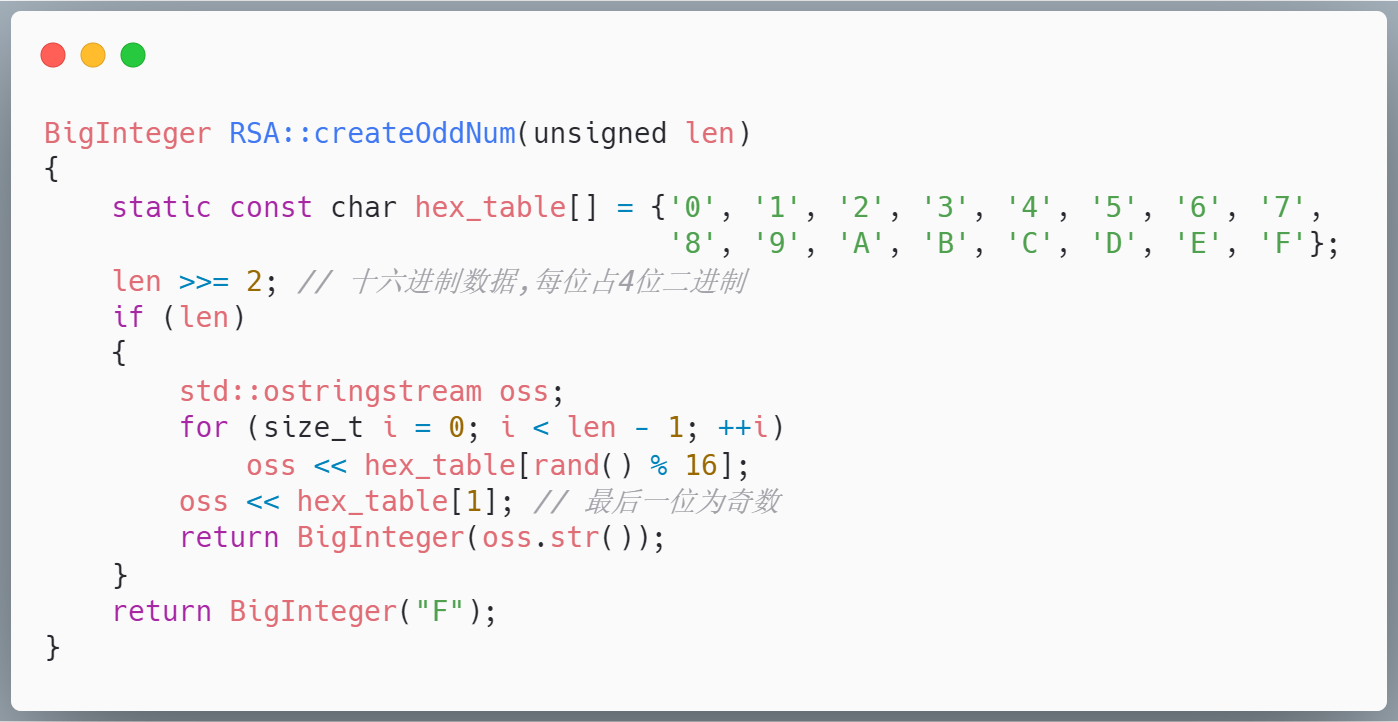
首先要生成密钥对,即生成公钥和私钥,那么,我们首先需要生成两个大素数p和q,显然,素数是不可能是偶数的,故定义一个生成随机奇数的函数BigInteger createOddNum(unsigned len)参数为奇数的长度。
使用16进制的随机字母,然后随机选取其中的len/4个得到一个随机的大奇数,只需要末尾那个数为奇数即可,最后返回BigInteger类型的奇数大整数,关键代码如下:

然后定义一个生成素数的函数,其中用到米勒-拉宾素性检验算法判断生成的素数是否为素数素数:
米勒-拉宾素性检测算法
基于以下定理:
- 费马小定理
要测试$N$是否为素数,首先将$N−1$分解为$2^{s}d$。在每次测试开始时,先随机选一个介于$[1,N−1]$的整数$a$,之后如果对所有的$r∈[0,s−1]$,若${a^d}\bmod N \ne 1$且${a^{{2^r}d}}\bmod N \ne - 1$,则$N$是合数。否则,$N$有$3/4$的概率为素数。
关键代码如下:
生成素数的逻辑就是首先使用函数createOddNum生成一个大奇数,然后调用isPrime判断是否为一个素数,是的话就可以return,不然继续寻找,知道生成一个素数。
接下来计算n值,n值的计算很简单,直接使用$n = p * q$ 这个式子就能够计算出来;计算欧拉值也一样,可以使用$\varphi(n) = (p-1) * (q-1)$得出。其中比较难的是生成的私钥d。
下面定义一个RSA类的初始化函数init(),生成p、q以及密钥对,如下:

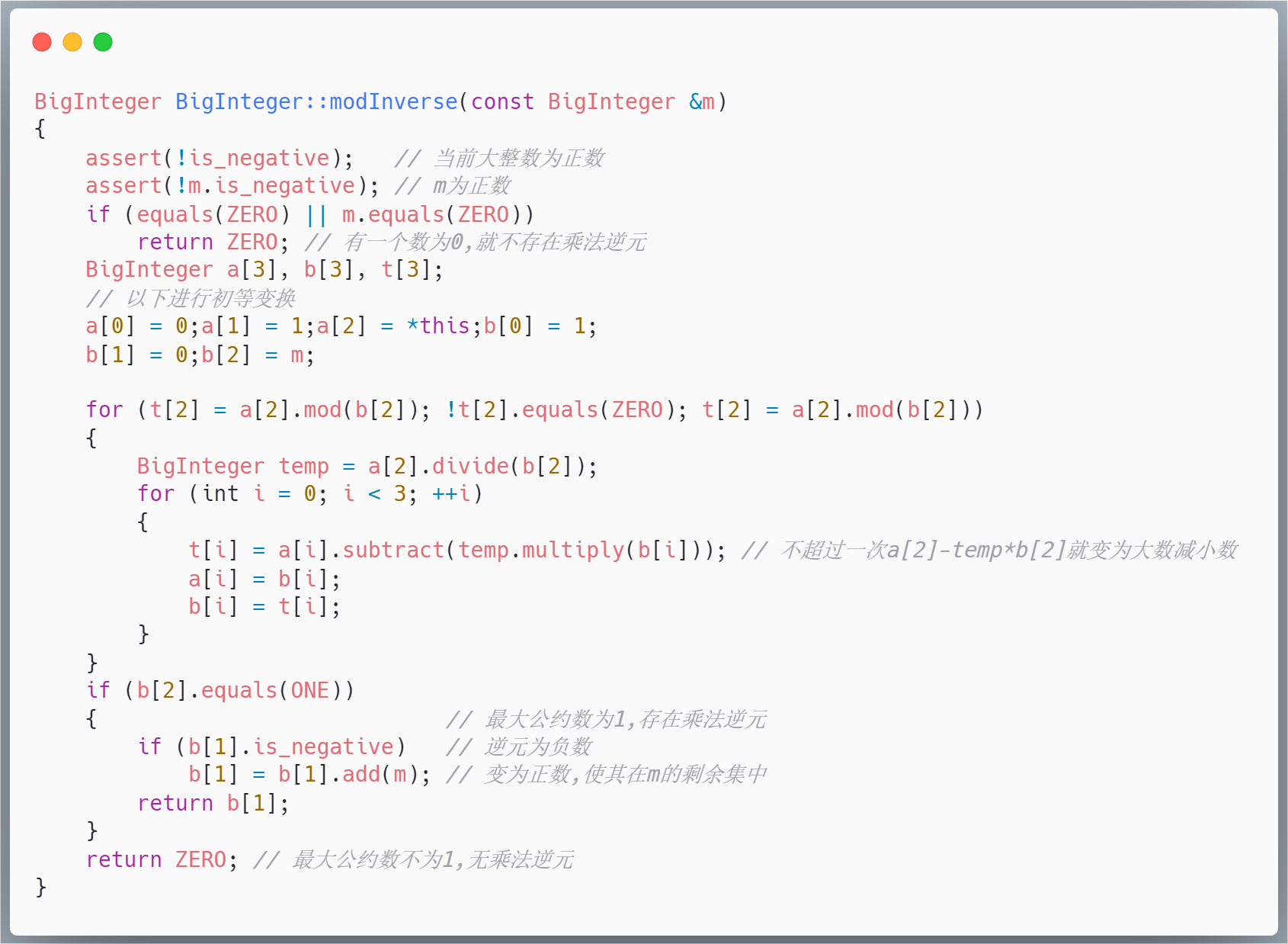
在创建公钥e和私钥d的函数createExponent(eul)中,首先创建一个比欧拉值小的公钥e,其中e为一个素数,直接调用函数createPrime()生成,然后使用大整数类中的求模逆元,即求出私钥d。
扩展欧几里得算法
逆元
逆元是模运算中的一个概念,我们通常说 A 是 B 模 C 的逆元,实际上是指 A * B = 1 mod C,也就是说 A 与 B 的乘积模 C 的余数为 1。可表示为 A = B^(-1) mod C。
打个比方,7 模 11 的逆元,即:7^(-1) mod 11 = 8,这是因为 7 × 8 = 5 × 11 + 1,所以说 7 模 11 的逆元是 8。
扩展欧几里得算法是欧几里得算法(又叫辗转相除法)的扩展。已知整数a、b,扩展欧几里得算法可以在求得a、b的最大公约数的同时,能找到整数x、y(其中一个很可能是负数),使它们满足贝祖等式
$$
ax{\rm{ }} + {\rm{ }}by{\rm{ }} = {\rm{ }}gcd\left( {a,b} \right).
$$
在RSA算法中求私钥中的整数d时,需要使得 (e * d ) % n = 1,该方程等价于 e * d = 1 + y * n (y为整数),也等价于 e * d - y * n = 1。
因此求解d的过程就是求解该二元一次方程组(e和n已知,求解d),即求e模n的逆元。
关键代码如下:

我们知道,RSA的加密与解密其实就是一个模幂的运算,而这个模幂的运算已经在大整数类中实现了,如下:
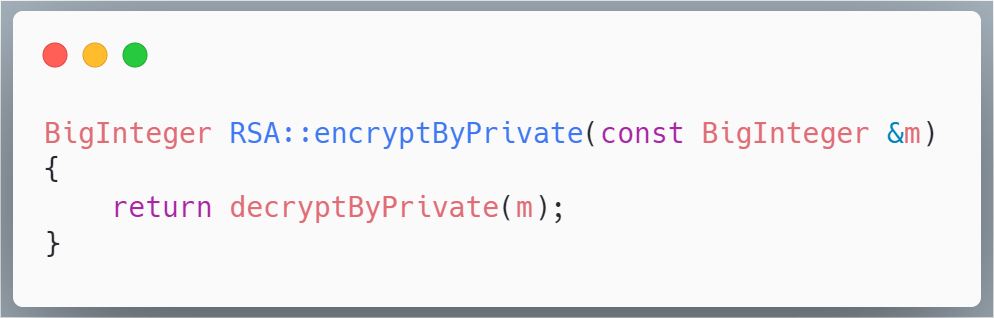
使用RSA类进行加密解密的函数只需要调用这个模幂运算即可,例如私钥加密可以这样调用:

以上就设计完了RSA类的相关操作,主要是包括密钥的生成。下面将RSA加密解密的操作封装在一个类中。
3. 设计加密解密类EncryptDecrypt
主要的方法及成员如下:
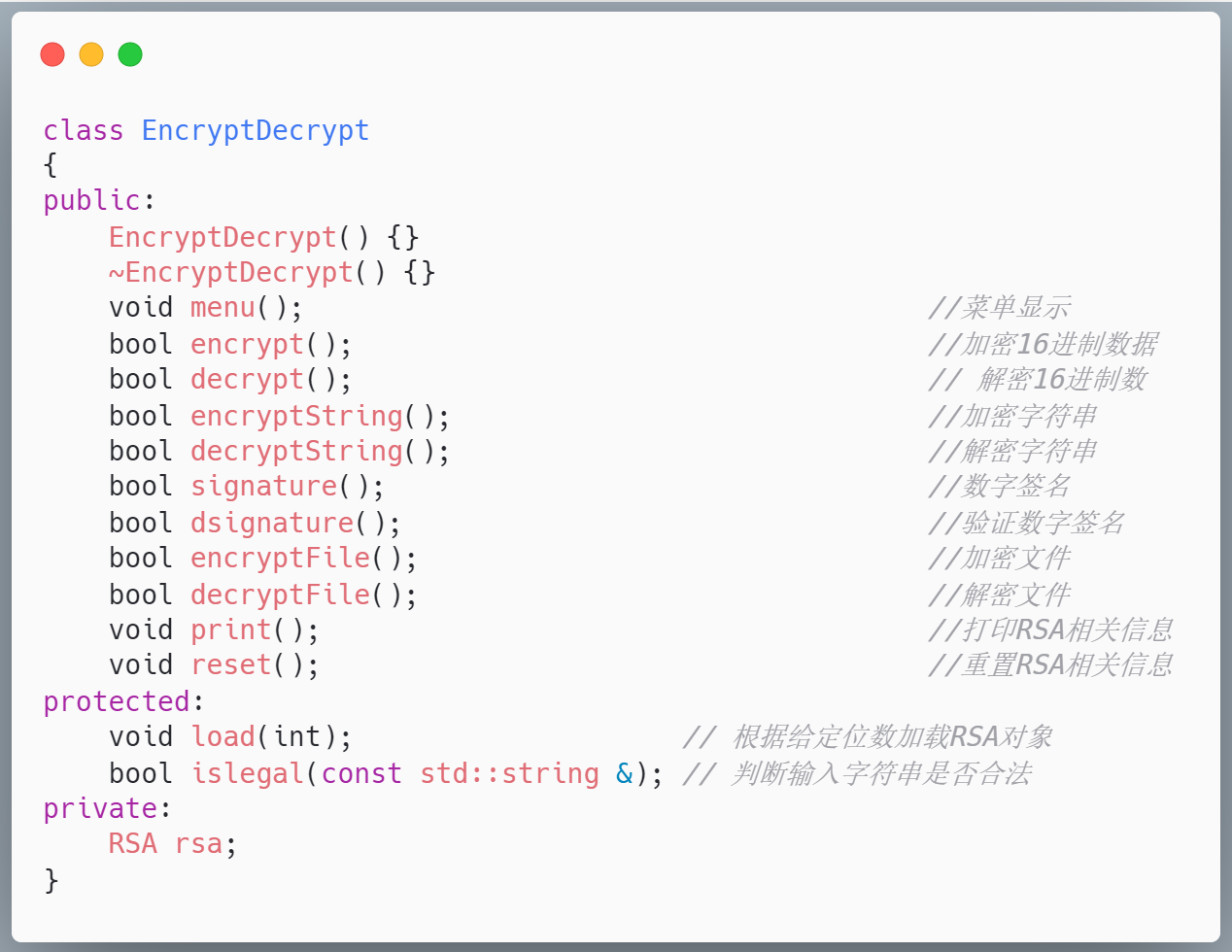
实现RSA加密解密字符串
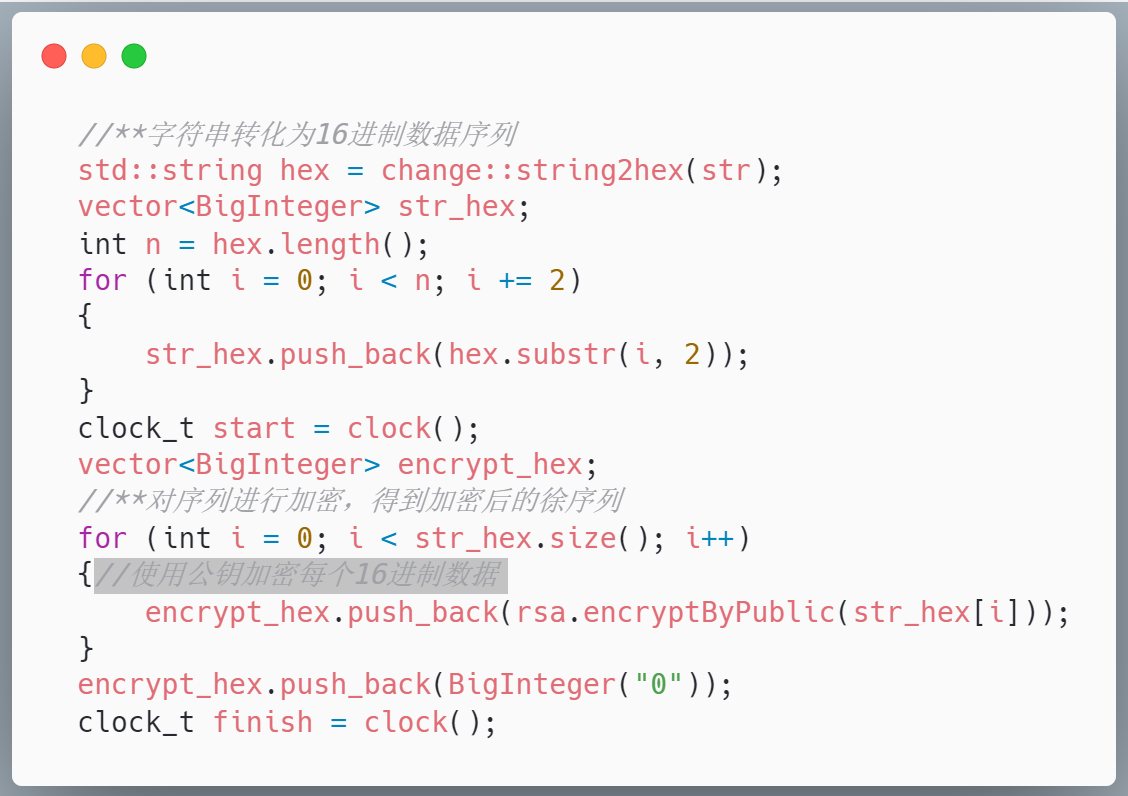
加密字符串的逻辑是,先将字符串以每两个字符 一组,转化为一个16进制数据序列,使用vector容器保存,之后调用rsa的公钥加密函数进行加密,如下是关键代码:
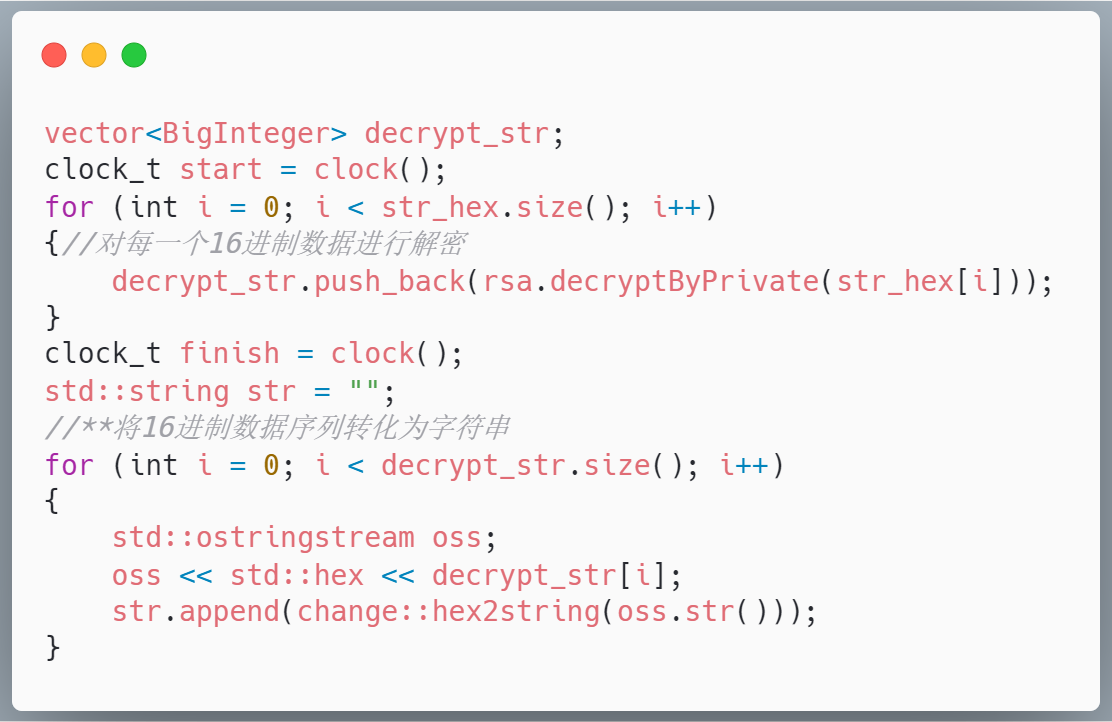
解密函数其实是接受一个加密后的16进制序列,然后对这个序列调用RSA的私钥解密函数进行解密,然后得到解密后的16进制数据序列,最后还有一步就是需要将这个16进制序列最终转化为原来的字符串,只需要根据ascii码的数值即可得到,这里编写了一个hex2string函数,关键代码如下:
实现效果
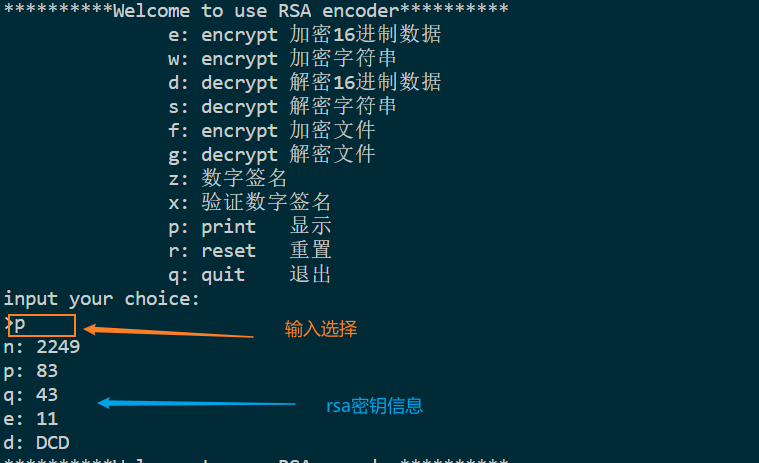
首先显示密钥:
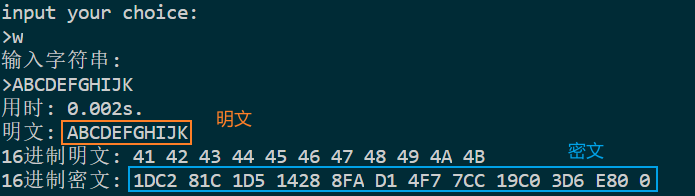
加密字符串
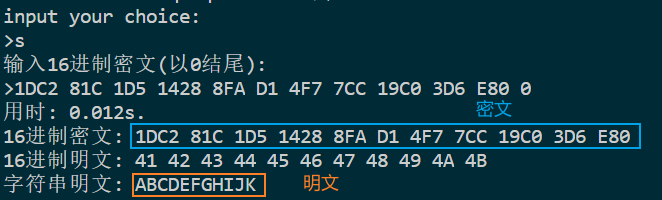
解密字符串
实现RSA加密解密文件
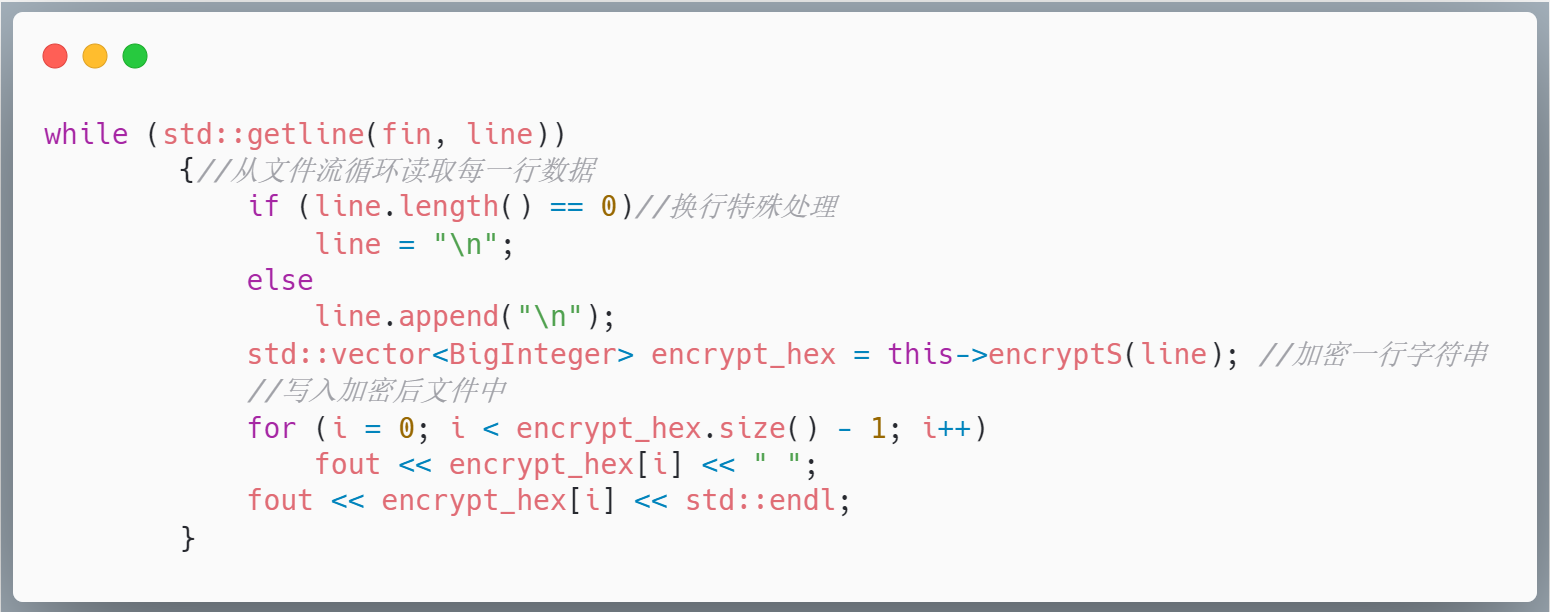
实现RSA加密解密文件时基于RSA加密解密字符串实现的,其中主要的加密逻辑就是将一个文件看作是一行一行的字符串文本,没每读取一行,就调用加密字符串的函数进行加密,然后将加密得到的16进制序列写入到另外一个文件中,而这个文件也就是加密后的文件,主要关键代码如下:

解密文件的函数稍微有点不一样,是从打开的待解密文件中循环读取每一个16进制数据,然后对每一个16进制数据调用解密函数得到解密后的16进制数据,将16进制数据转为字符串后再相继的写到另外一个文件中,即解密后的文件,关键代码如下:
实现效果
加密文件
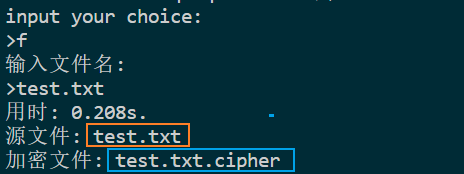
解密文件
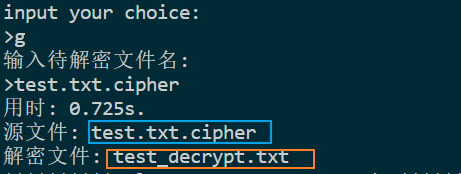
加密文件解密文件对比
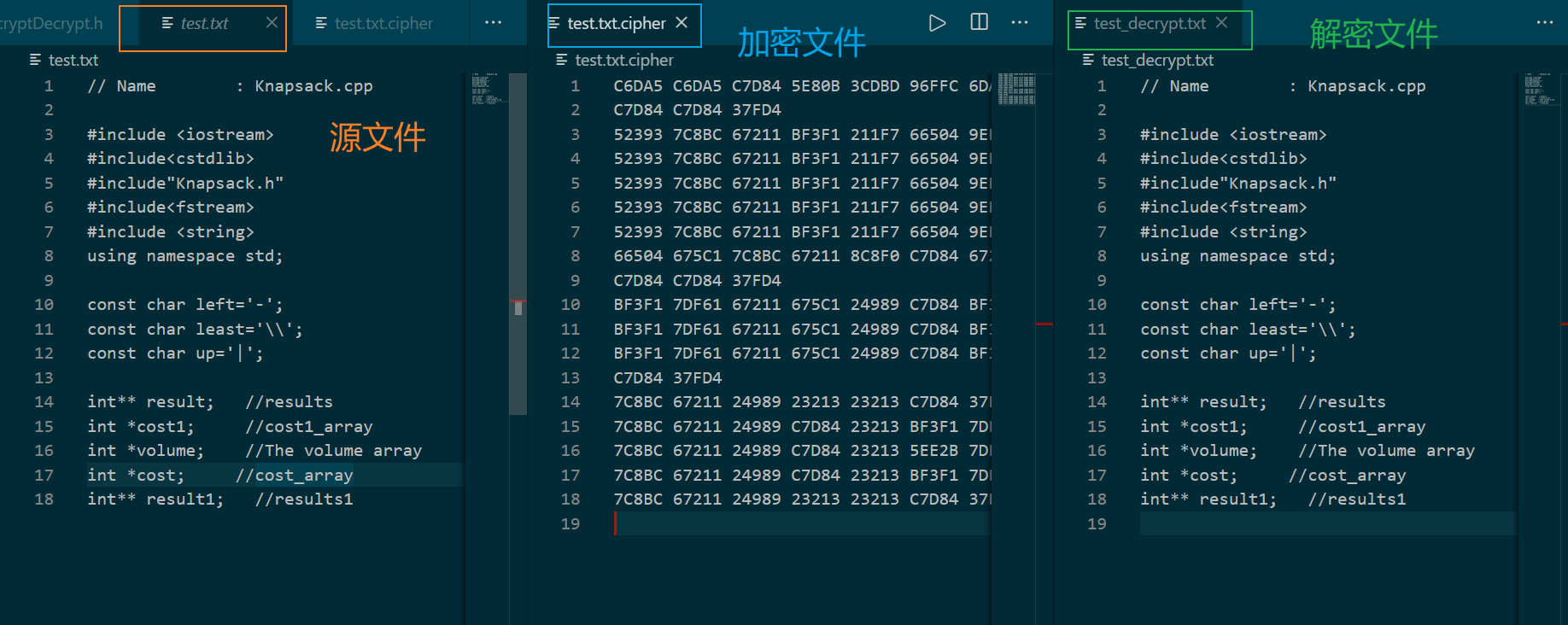
实现RSA数字签名及验证
实现数字签名方案,按照以下的流程图进行操作。
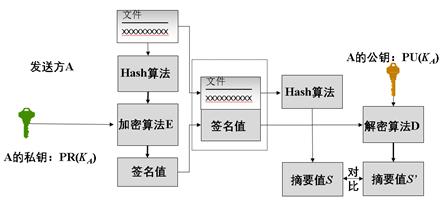
首先需要对文件进行信息的摘要,得到Hash值,这里选择的Hash算法是SHA512算法,可以直接对文件进行信息摘要。
可以直接include C++ 实现的"sha512.h"文件头,然后使用以下的语句就能够生成一个长度为512的Hash值,如下:
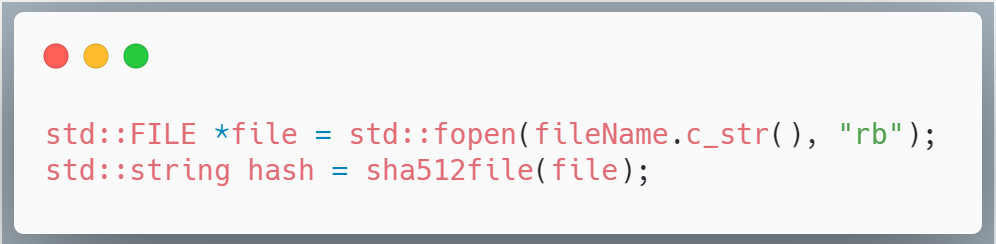
可以在命令行输出文件的Hash摘要值如下:

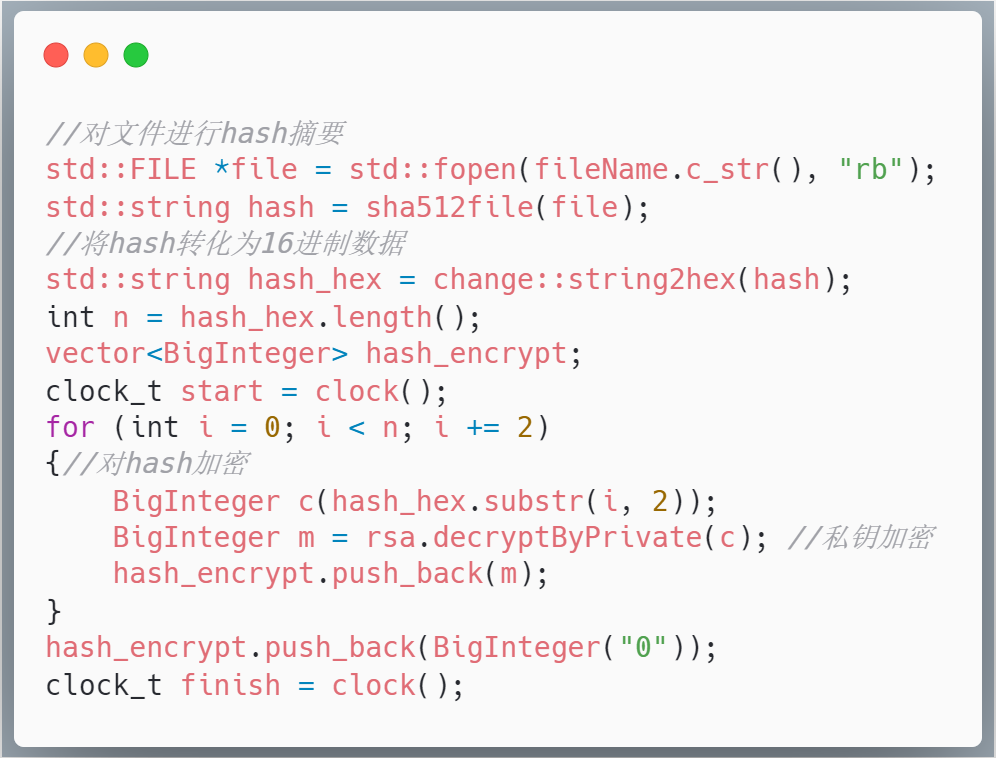
数字签名的实现类似字符串加密,对文件的hash值进行加密得到后面的16进制序列,然后将16进制序列伴随文件发送出去,签名的关键代码就是对hash值进行加密,如下:
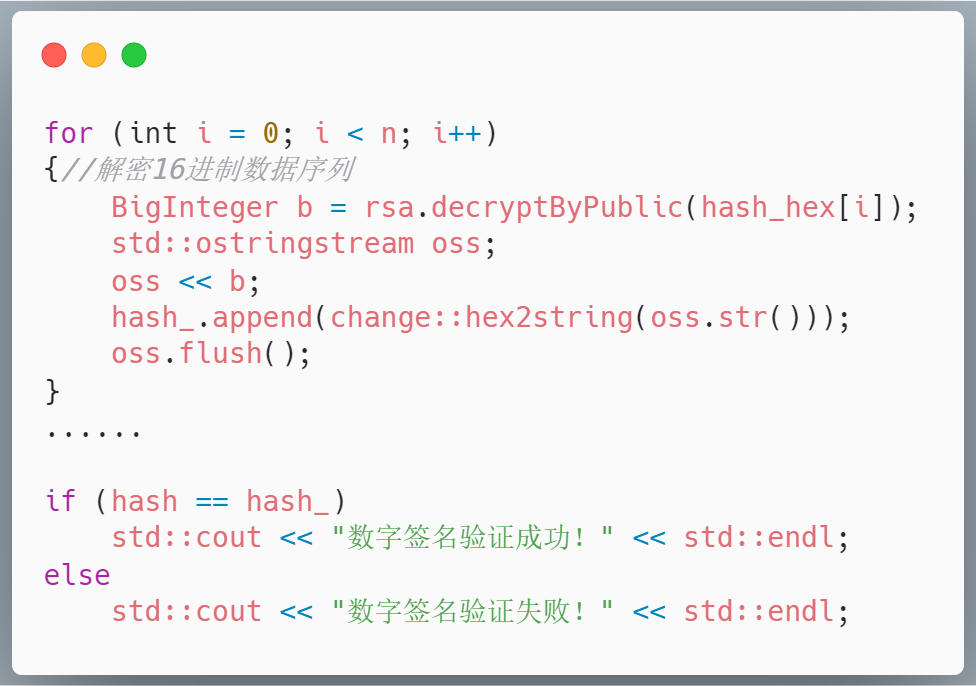
验证函数直接将16进制序列进行解密,然后还原成字符串再与收到的文件的hash值进行比较,如果相等,那么验证成功;否则验证失败,关键代码如下:
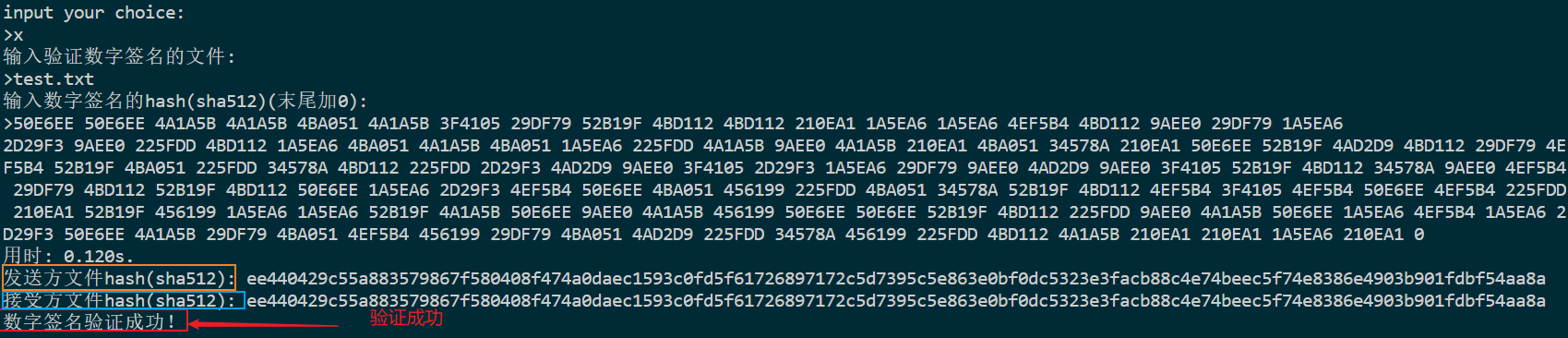
实现效果
数字签名

验证数字签名